The inherent structure of human cognition facilitates the hierarchical organization of semantic categories for three-dimensional objects, simplifying the visual world into distinct and manageable layers. A vivid example is observed in the animal-taxonomy domain, where distinctions are not only made between broader categories like birds and mammals but also within subcategories such as different bird species, illustrating the depth of human hierarchical processing. This paper presents Deep Hierarchical Learning (DHL) on 3D data, a framework that, by formulating a probabilistic representation of hierarchical learning, lays down a pioneering theoretical foundation for hierarchical learning (HL) in 3D vision tasks. On this groundwork, we technically solve three primary challenges: 1) To effectively connect hierarchical coherence with classification loss, we introduce a hierarchical regularization term, utilizing an aggregation matrix from the forecasting field. 2) To align point-wise embeddings with hierarchical relationships, we develop the Hierarchical Embedding Fusion Module (HEFM) as a plug-in module in 3D deep learning, catalyzing enhanced hierarchical embedding learning. 3) To tackle the universality issue within DHL, we devise a novel method for constructing class hierarchies in common datasets with flattened fine-grained labels, employing large vision language models. The above approaches ensure the effectiveness of DHL in processing 3D data across multiple hierarchical levels. Through extensive experiments on three public datasets, the validity of our methodology is demonstrated. The source code will be released publicly, promoting further investigation and development in hierarchical learning.

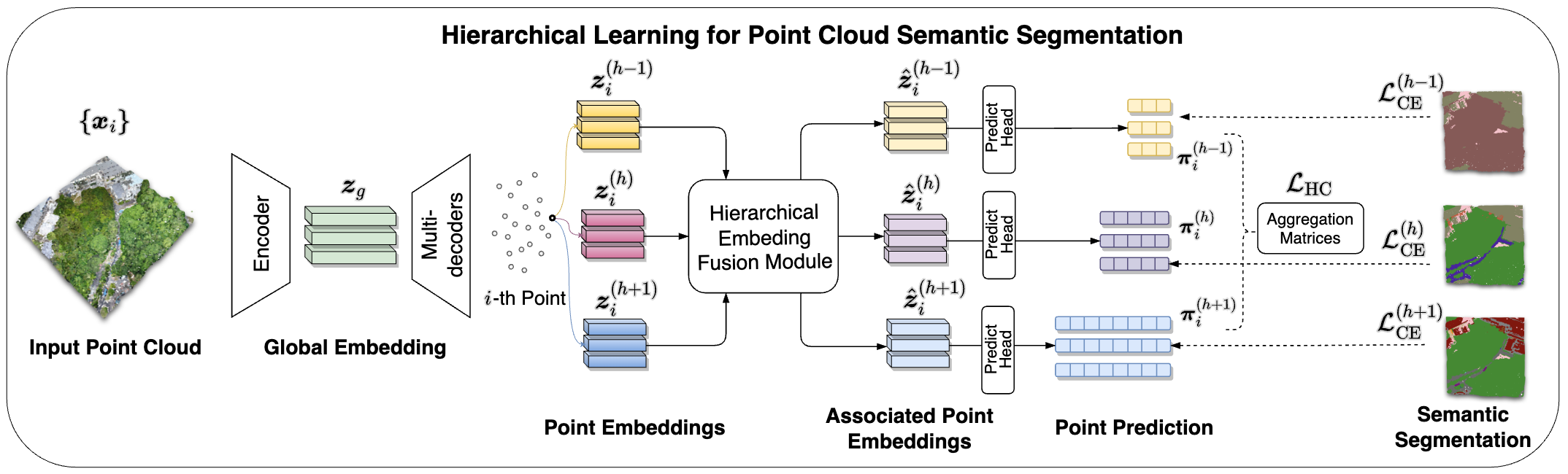
This architecture takes the raw point cloud as input and facilitates the learning of hierarchically coherent predictions. It consists of three key components:

• Encoder and Multi-Decoders (EMD): The EMD is a multi-task learning network that incorporates a shared encoder and multiple parallel decoders, with each decoder corresponding to a hierarchical layer. In Section V, we explore the use of three popular 3D segmentation backbones as encoders, including PointNet++, RandLANet, and SparseUNet. The EMD focuses on encoding geometric information while disregarding the rich semantic relations among classes at different hierarchical layers simultaneously.


• Hierarchical Embedding Fusion Module (HEFM): The HEFM leverages structured knowledge (i.e., TDCC and BDCC) to reshape point embeddings, generating hierarchy-aware point representations and enhancing coherence in predictions


• Hierarchical Coherence (HC) Loss: Our proposed network is trained end-to-end by minimizing a combination of the HC loss and cross-entropy loss.

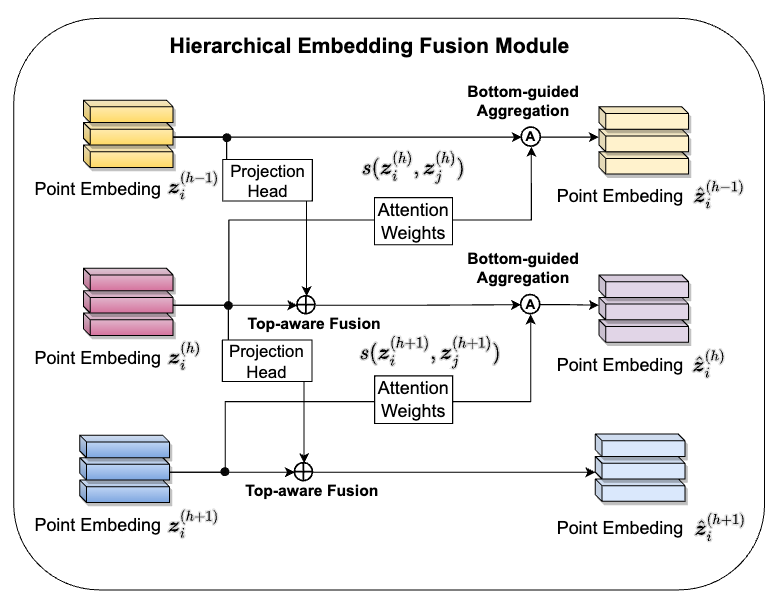
The TDCC and BDCC constraints outline the necessary conditions for hierarchically coherent predictions. We contemplate employing them BDCC as constraints for HL. However, direct utilization of TDCC and BDCC is challenging and redundant for the loss in Section 4.3. We consider adapting them into soft constraints for multiple samples, i.e., inter-points constraints. The specific expression of this adaptation is that if two points have inconsistent predictions at the super-class layer, their predictions at the sub-class layer must be inconsistent as well; if their predictions at the sub-class layer are consistent, then their predictions at the super-class layer must also be consistent. These constraints are integrated into the Hierarchical Embedding Fusion Module (HEFM). The HEFM comprises two essential components:

• Top-aware Fusion: It ensures that points associated with the same super-class labels in the top-level should be proximate to each other within the embedding space of the bottom-level.


• Bottom-guided Aggregation: It enforces that points linked to the same subclass labels in the bottom-level should exhibit similarity within the top-level embedding space.

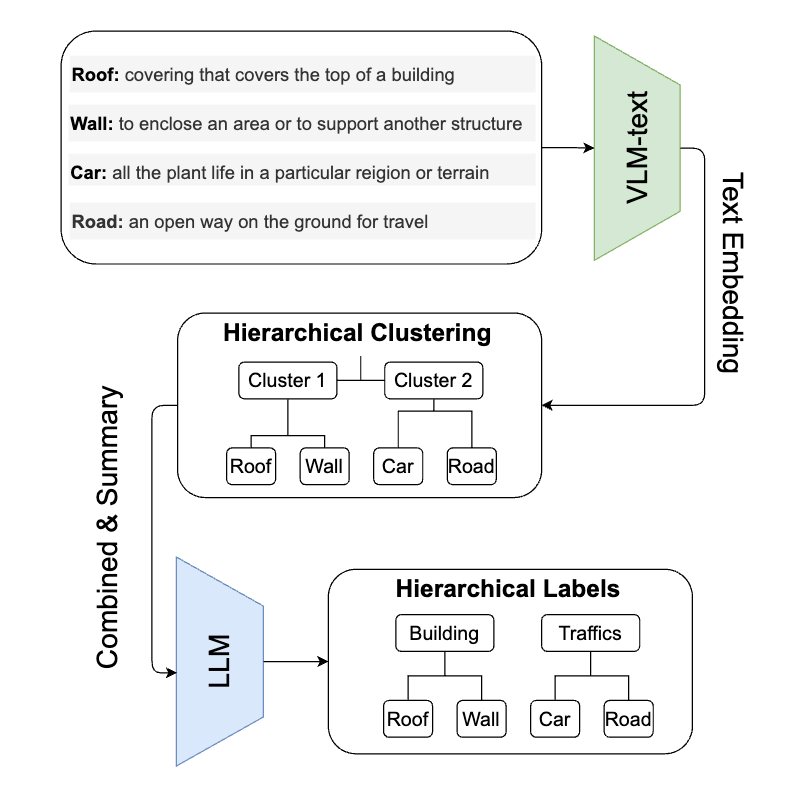
The preceding sections detailed a method for training segmentation models on hierarchically annotated 3D datasets. Yet, the significant annotation effort required for such datasets often limits their availability. To broaden our approach’s applicability, we introduce a technique to construct a class hierarchy from the fine-grained class labels within the dataset. Our methodology exploits a Vision Language Model (VLM) to derive class embeddings. Subsequently, these embeddings inform a hierarchical clustering process, producing a dendrogram of classes. It’s essential to underscore that constructing a label taxonomy for hierarchical 3D segmentation should account for both the semantic relevance and the geometric characteristics of the class. Recent advances in VLMs, particularly in aligning geometric features in images with language embeddings, enable us to harness pre-trained embeddings for this hierarchy extraction. We utilized the widely-acknowledged CLIP text encoder, trained on the WebImage Text Dataset, to encode the fine-grained classes present in the 3D dataset. For improved precision, we employed the dataset’s class definitions as caption text, rather than solely the class terms, thus mitigating potential word embedding ambiguities. These embeddings then serve as features, guiding the iterative merging of clusters from the original fine-grained classes into a class dendrogram. Ultimately, we employ a large language model (LLM) to prune the generated dendrogram, resulting in a semantically coherent class hierarchy.

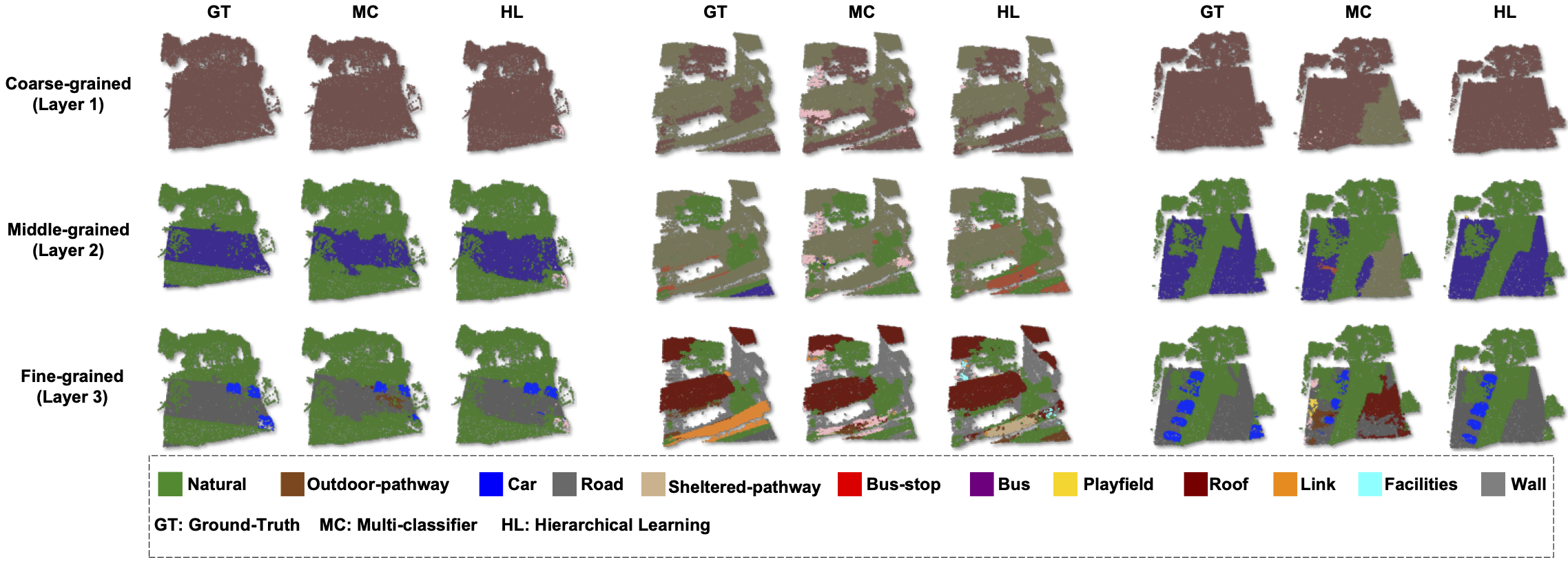
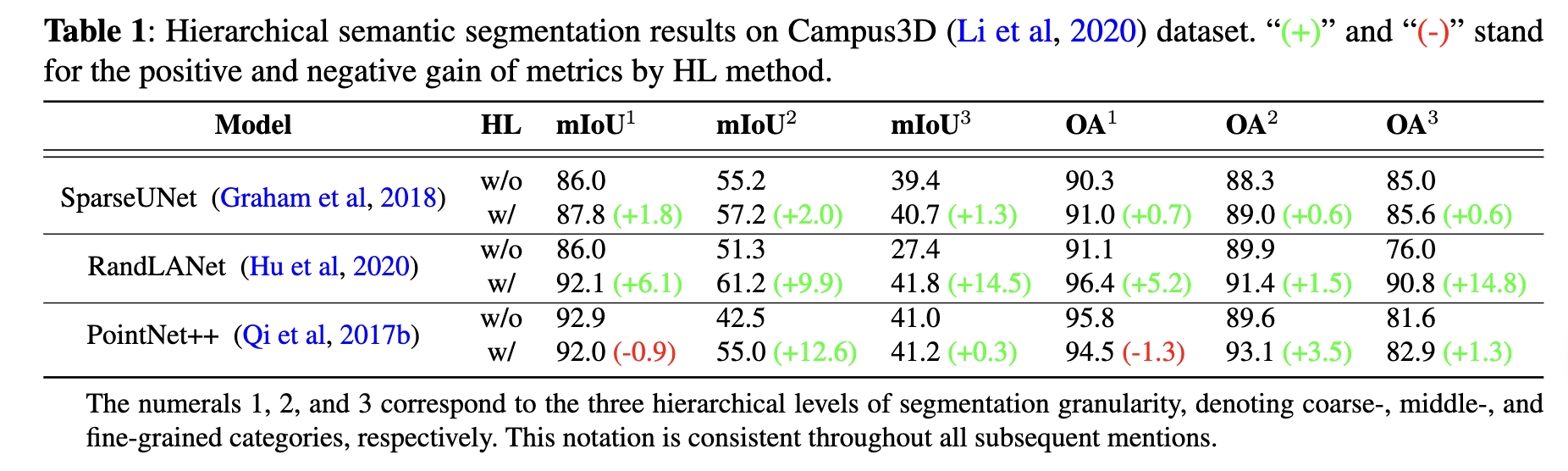
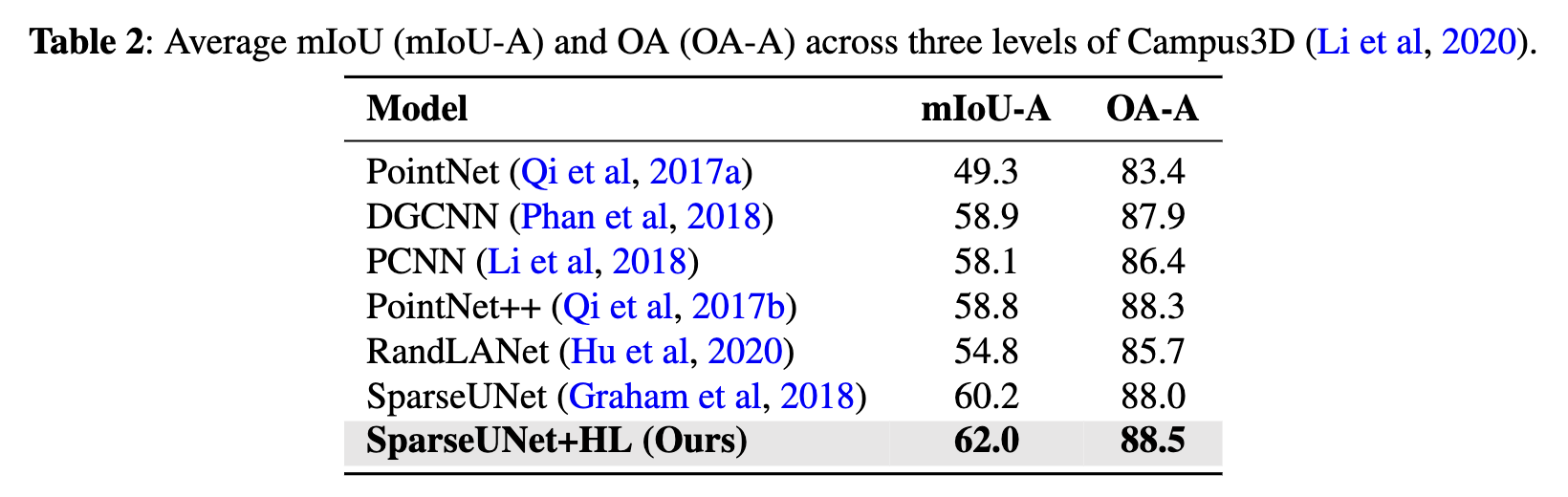
Across nearly all hierarchical levels and models, we observe consistent performance gains when employing HL. The sole deviation from this trend is with the multi-classifier variant of PointNet++ (i.e., PointNet++ without HL), which outperforms its HL counterpart at the most coarse-grained level. A potential explanation for this could be that the inherent structure and feature representation of the raw PointNet++ model is better suited for coarse-grained segmentation tasks, whereas HL might introduce complexities that marginally diminish performance at that specific level. Nevertheless, the overall superior performance of the HL mechanism over the traditional multi-classifier underscores its potency in 3D hierarchical semantic segmentation. A potential explanation for the HL method’s enhanced performance is that the intrinsic relationships among hierarchical label layers may provide supplementary geometric information beneficial for semantic segmentation.

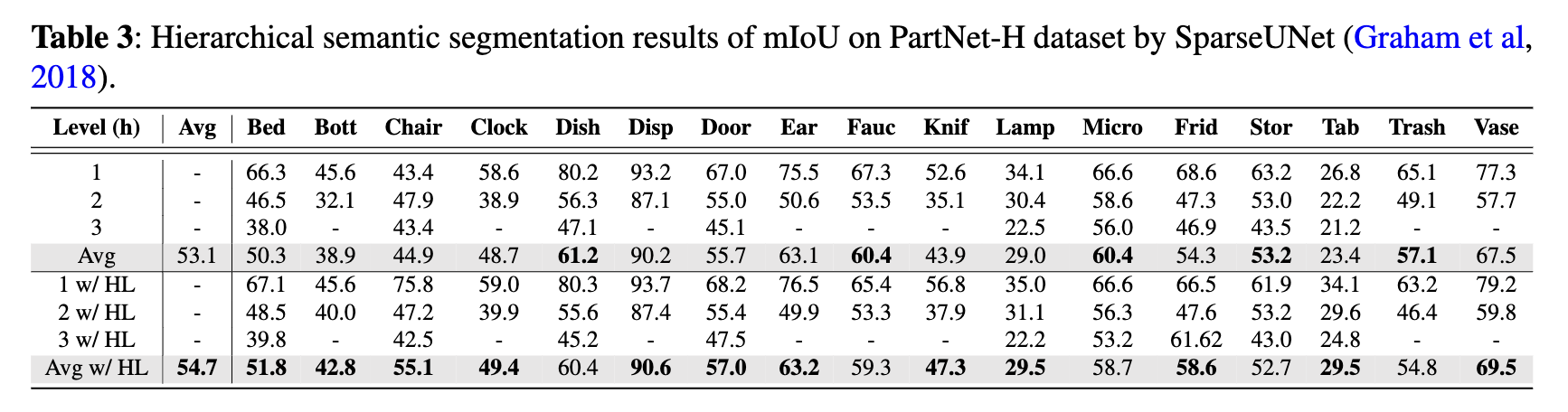
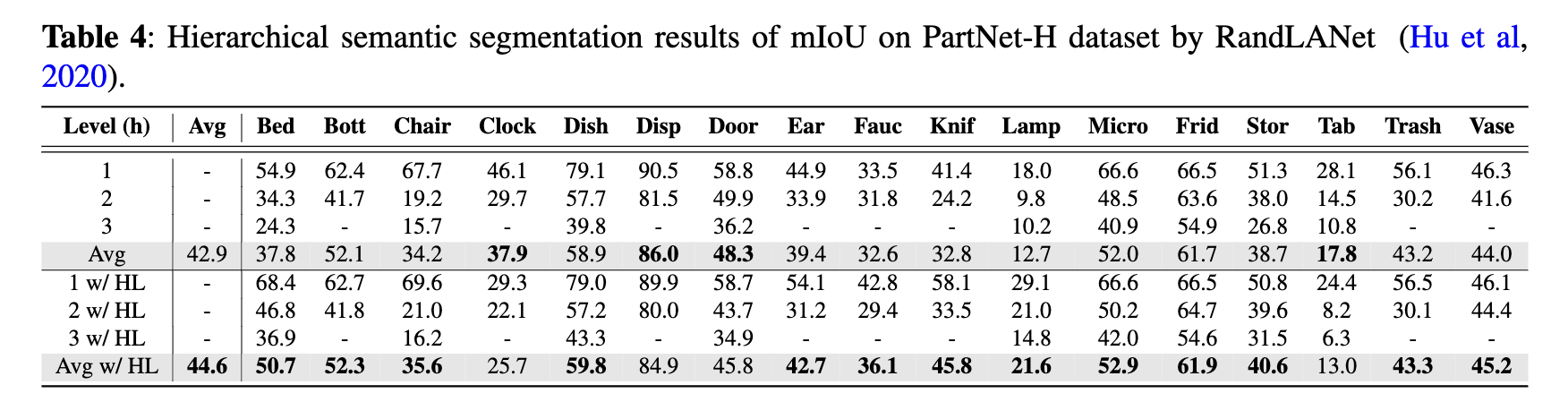
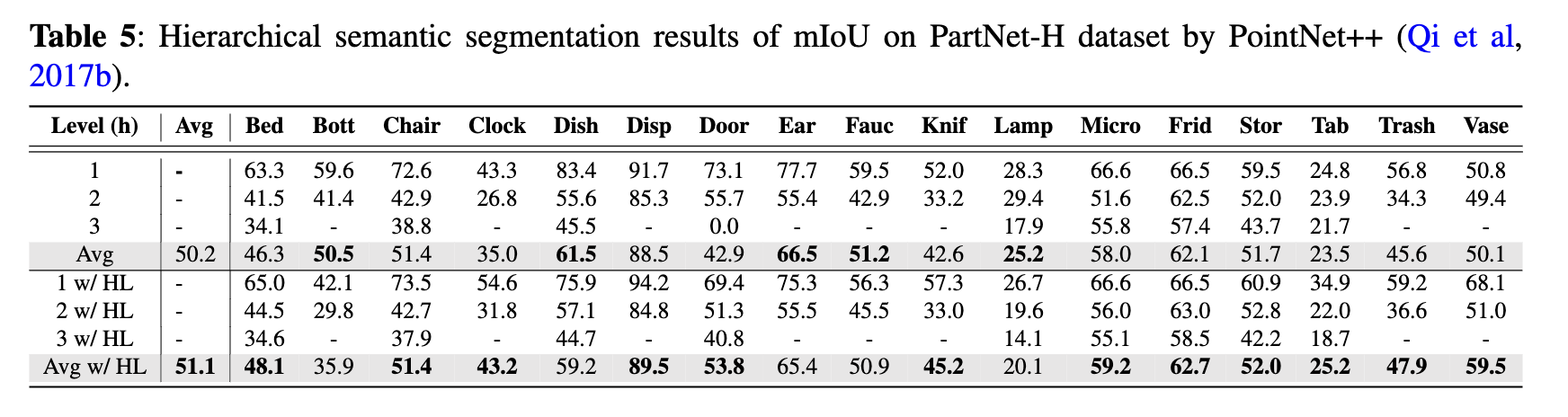
Results for the three models, both with and without HL, can be found in Tables 3 through 5. The mIoU has been computed for each of the 17 part categories as well as the average across three levels of segmenta- tion: coarse-, middle-, and fine-grained. From the data in Tables 3 to 5, it’s evident that SparseUNet, Rand- LANet, and PointNet++ models equipped with HL outperform their non-HL counterparts in 12, 13, and 12 categories, respectively, in terms of mIoU. Additionally, HL has been shown to improve the average mIoU across all 17 categories by approximately 1% to 2%, further underscoring the benefits of its integration. Significant observations include: 1) the class categories that have shown improvement with HL vary considerably among different backbone models, such as SparseUNet, RandLANet, and PointNet++, and 2) there are certain categories where HL did not enhance performance. These variations suggest that HL’s effectiveness is not uniform across all categories and may be influenced by the inherent characteristics of the backbone models. This variability indicates a good generalization capability of HL, as different models, with their unique strengths and weaknesses, may inherently perform well or poorly on certain class categories.

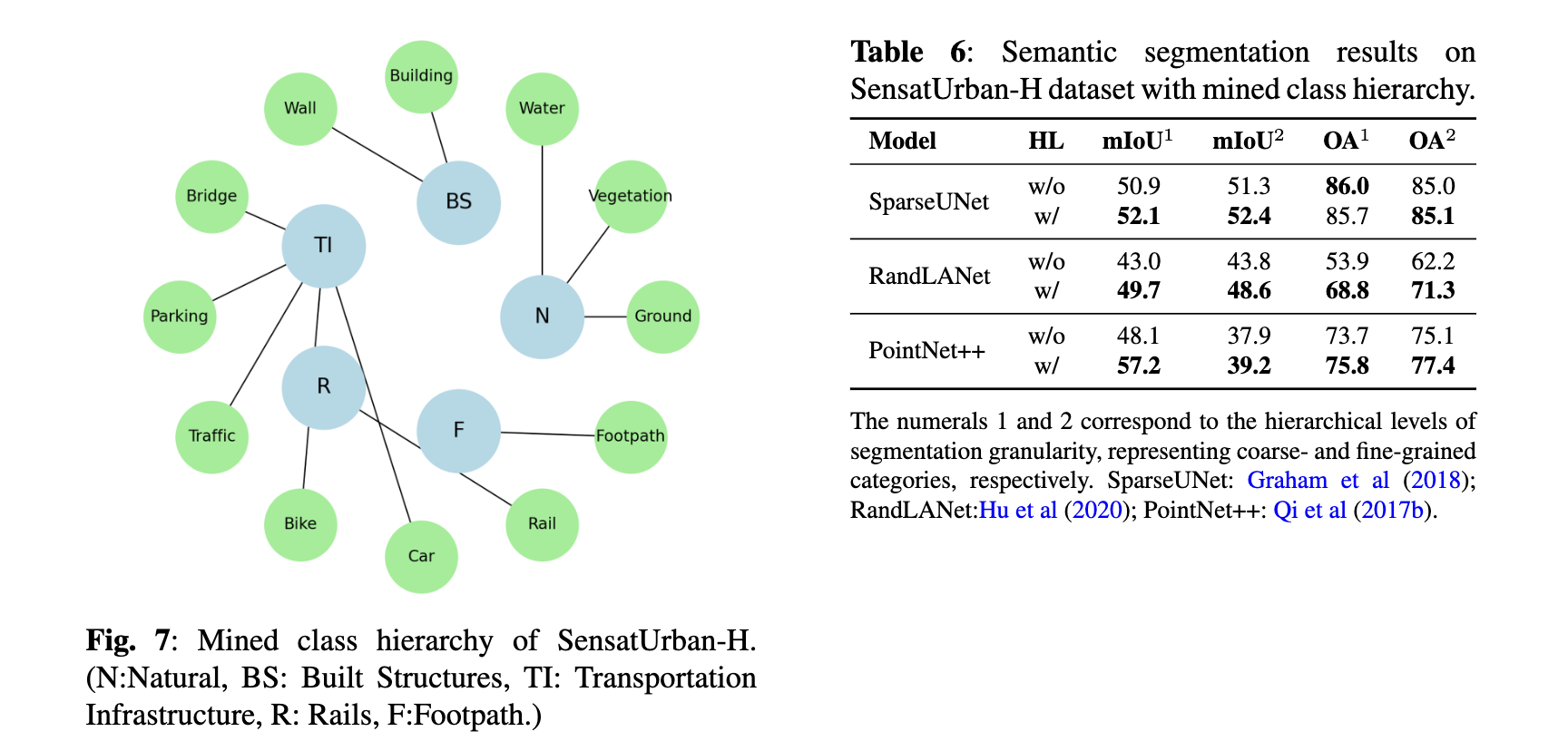
In this subsection, we evaluate the proposed HL approach on another 3D dataset, SensatUrban (Hu et al, 2021). This dataset is not originally annotated in a hierarchical manner. To create a hierarchical structure, we employ our class hierarchy mining method (refer to Sec. 4.4), generating a two-level class hierarchy, which is displayed by Fig. 7. The enhanced dataset, which we denote as “SensatUrban-H”, will be publicly available once the paper is accepted. Semantic segmentation results for SensatUrban- H are presented in Table 6. Aside from the OA of SparseUNet at the coarse-grained level, HL has led to significant improvements. Most notably, in the finegrained (level 2) segmentation task, HL boosts the performance of RandLANet by over 15% in terms of mIoU and around 9% in terms of OA.